Arcetri High Energy Group

GRMHD

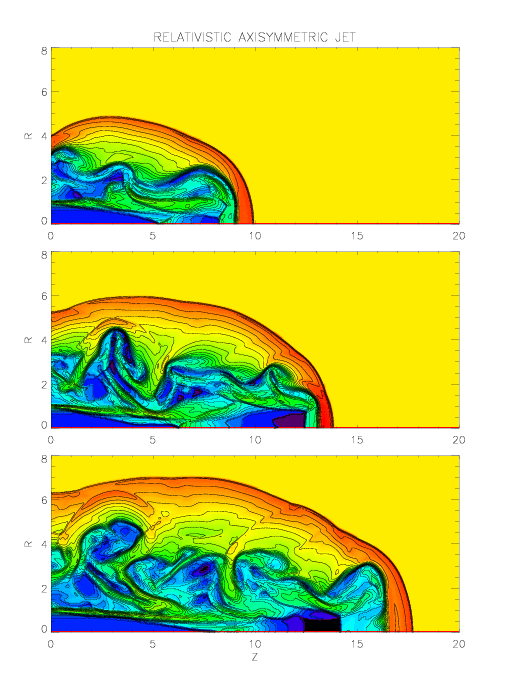
Most of the astrophysical sources of high-energy radiation and particles are believed to involve the presence of relativistic motions in magnetized plasmas. For example, the radio emission from extra galactic jets (especially from terminal radio lobes) or from plerionic supernova remnants (e.g. the Crab Nebula) is due to synchrotron radiation produced by relativistic electrons spiraling around magnetic field lines, thus indicating the presence of significant magnetic fields. Strong magnetic fields are supposed to play an essential role in converting the energy of accreting material around super-massive black holes at the center of Active Galactic Nuclei (AGNs), into powerful relativistic jets escaping along open field lines. Similar phenomena may be at work in the galactic compact X-ray sources known as microquasars and even in Gamma Ray Burst (GRB) engines. These processes involve highly nonlinear interactions of relativistic gasdynamic flows and shocks with gravitational and magnetic fields. The fluid approximations employed to study the dynamics of relativistic plasmas are special relativistic MHD (SRMHD) and general relativistic MHD (GRMHD), the latter in the case when the curvature of space-time becomes significant in the vicinity of a compact object. A strong impulse to the study of these complex phenomena has come from numerical simulations, especially in the last decade. Since relativistic magnetized flows are often associated with the formation of strong shocks and different kinds of discontinuities, it is thanks to the development of conservative shock-capturing, or Godunov-type, methods that this progress has been possible. After the first applications to special and general relativistic hydrodynamics, Komissarov (1999) first proposed a multi-dimensional shock-capturing code for SRMHD based on the so-called Roe-type methods, widely used in computational gas dynamics, in which the solution of the local Riemann problem at any cell interface is constructed by means of a full decomposition into characteristic waves (note that the SRMHD eigen-structure is not solvable analytically, contrary to classical MHD). Accurate and robust Riemann solvers for SRMHD requiring fewer eigen-modes have been also recently developed. Relying on the promising results obtained for classical MHD members of our group first proposed a different approach for SRMHD: one or two-wave Riemann solvers are used component-wise in combination to higher-order spatial upwind reconstruction (third order at least). This latter scheme has also been extended to GRMHD, and to the case of an evolving spacetime metric. Most of the codes available nowadays for SRMHD and GRMHD make use of a simplified Riemann solver. The numerical code developed and used by our group has been named ECHO (Eulerian Conservative High Order code), it is written in Fortran90 using a modular approach, and solves the set of hyperbolic conservative equations in the so-called 3+1 formalism, in which space and time are clearly disentangled. 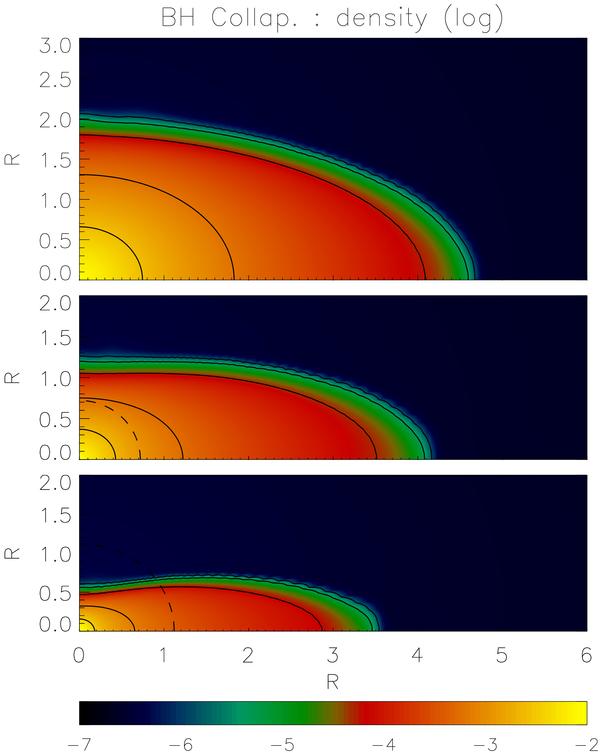For evolving spacetimes, Einstein equations are solved in axisymmetric configurations under the Conformally Flat Condition (CFC), appropriate for studying isolated neutron stars and black holes. Initial conditions for magnetized neutron stars are provided by the publicly available XNS code