XNS

Equilibrium models for neutron stars requires the symultaneous solution of Einstein's Equations, that describe the space-time metric, and of the Magneto-Hydrostatic Equilibrium, that provides the distribution of matter/energy.

For what concerns the solution of Einstein's Equations , the assumption on which the metric solver unsed by XNS operates is that the spatial metric is conformally flat (CFC), such that in spherical coordinates the line element can be written as:

where α is the lapse function, ψ is the conformal factor, and β the shift vector. This assumtion allows us to simplify the Einstein's equations, that now reduce to a set of elliptical partial differential equations, cast them in a numerically stable form and, as a consequence, handle stronger fields and deformations that in a perturbative approach can not be obtained, without compromising the accuracy of our results as we will discuss. A full descritption of this strategy and of the metric solver can be find in.

Concerning the distribution of matter and fields, the basic assumtion is that it can be described in terms of ideal MHD. In particular we assume that the energy-momentum tensore has the form:

where e is the energy density, p is the pressure, b the comoving magnetic field, and g the metric tensor. It is possible to show that under specific conditions (i.e. for a barotropic fliud) the Equilibrium equations admits an integral form known as Bernoulli's Integral. This allow to related conditions at any point in the star to conditions in the very center. The form of Bernoulli's Integral depends on the assumtions about the rotational prpoperties (uniform vs differential), on the structure and geometry of the magnetic fieldf (how matter and el;ectric currents are related). The derivation of the Bernoulli's Integral, and a broad set of functional forms describing several differetn magnetic configuration used by XNS can be found in. and in.

The complete algorithm of the metric solver is fully presented in Bucciantini & Del Zanna (2011). The GRMHD equations in the 3+1 formalism used by the XNS code can be found in Del Zanna et al. (2007). The XNS code is fully described in Pili et al. (2013). The equation for the metric terms can be cast in the form of Poisson-like equations. These are then solving using a strategy known as eXtended Conformally Flat Condition (XCFC) that allows one to cast them in a numerically stable form, and to decuople them so that they can be solved hierarchically.

Solutions, for the scalar quantities of interest (i.e. ψ and αψ), are searched in terms of a series of spherical harmonics. The Laplacian can then be reduced to a series of radial 2nd order boundary value ODEs for the coefficients of each harmonic, which are then solved using tridiagonal matrix inversion, on the same radial grid where the solution is discretized. Given that the equations are non-linear this procedure is repeated until convergence, using in the source term the value of the solution computed at the previous iteration.

The equation for the shift-vector (to be more precise the φ component) can be reduced to the solution of a linear vector Poisson equation. Interestingly, if a poloidal field is present, also the Grad-Shfranov equation, that describes the equilibrium condition for the magnetic part can be reduced to the solution of a non-linear vector Poisson equation, which is formally equivalent to the equation for the shift-vector (to be more precise the φ component), so that the same elliptic solver is used. The solution of the vector quatities is searched in terms of a series of vector-spherical harmonics.

The use of spherical harmonics allow us to preserve the correct behaviour on axis, the correct parity at the center, and the correct asympthotic trend at the other radius, without the need to use a compactified domain. In all of our models we have verified that 20 spherical harmonics are sufficient to achieve convergent results, even for the most extreme configurations with the discretization errors of our solutions are <10^-3.

This is a comparison of the results obtained by the XNS code with those of other codes presented in the literature. This is both a check on the performance of our algorithm and the numerical code, and a check on the quality and accuracy of the CFC (XCFC) approximation, given that the results we compare against, are derived in the exact regime for the space-time metric.

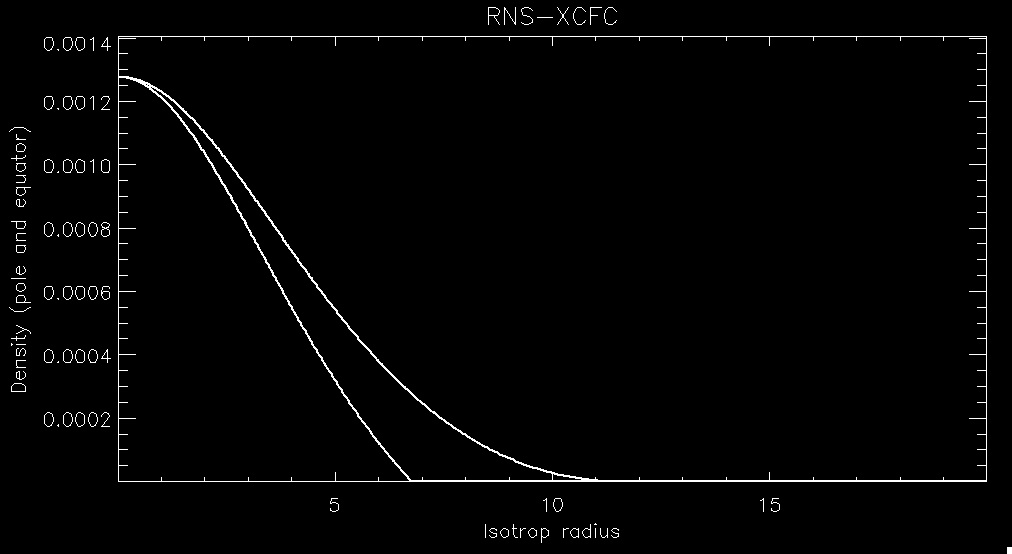
These are some comparisons with the code RNS, for a uniform rotator close to mass shedding limit. You can see that the errors are ~0.1% or smaller. On the left is a comparison of the polar, and equatorial densities: the solid lines are from RNS and the dashed lines (can you see them?) from XNS. On the right is a comparison of the errors in the metric terms. All the lines that you see represent various metric terms (see the Guide for explanation). They are all < 0.1%, the dash dotted line is a measure of how far from conformally-flat the RNS result is. That indicates the quality of the CFC/XCFC approximation.

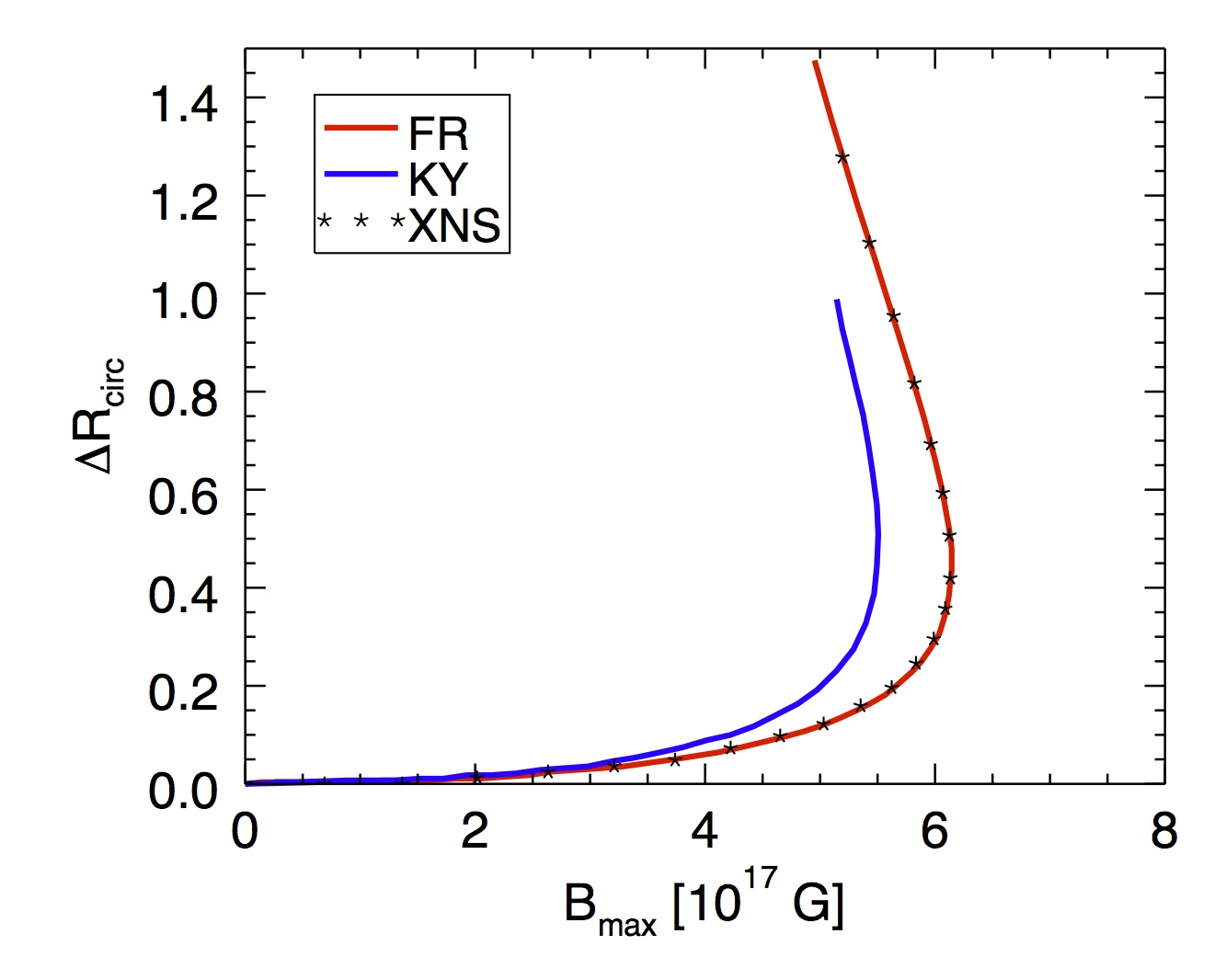
These are insted some comparisons with the recent results by for static configurations with purely toroidal magnetic field. A comparison with previous resutls by Kyuchi & Yoshida (2008 KY) and by Frieben & Rezzolla (2012 FR) is also shown. Strangely the results previoulsy shown in the literature are derived in the same regime, and solving analogous equations, yet the derived model are different. This shows that accuracy and stability of the numerical scheme are important to get a correct solution. XNS results are fully consistenn within a typical ~0.1% accuracy with the more recent results by Frieben & Rezzolla (2012)

A few good books on 3+1 Formalism and GRMHD

Some very good review papers on NSs models